
However, this textbook does not present a full discussion of control theory and related methods for system analysis.įor further reading, consult with references cited in this chapter. In this section, we present a brief background of frequency analysis and methods with focus on Bode plot method and transfer function, with worked-out examples. For example, identifying characteristics of a system-such as its natural frequency, behaviour at large and small frequencies, and magnitude of certain quantities at specific frequencies-provides useful insights in terms of system analysis, design, and control. Therefore, transforming the domain of analysis from time to frequency provides us with useful and important information about the behaviour of systems. However, when a system behaves in a repetitive mode under some applied load and/or boundary conditions-a quasi-static mode-we are interested in the changes in terms of the inherently-involved frequencies of the system rather than the details of instantaneous variations with respect to time. Studying the behaviour of systems with respect to time is the primary approach for systems modelling and analysis.
2.17 Example: A Pendulum with Moving Pivot.2.16 Example: A Complex Vibrating Mechanical System.2.15 Example: Atwood’s Machine with Massive String and Pulley.2.14 Example: A Compound Atwood’s Machine.2.13 Example: A Two-Loop Electrical Circuit.2.12 Example: A System with Energy Dissipation and Applied External Force.2.11 Example: A Multi-Mass-Spring System.2.10 Systems with Higher Order Equations.2.8 Alternative form of Lagrange’s Equation.2.7 Conservative and Non-Conservative Forces.2.5 Hamilton’s Principle and Lagrange’s Equations.2.4 Generalized Coordinates, Momenta, and Forces.2.3 Lagrange’s Equations for a Mass System in 3D Space.
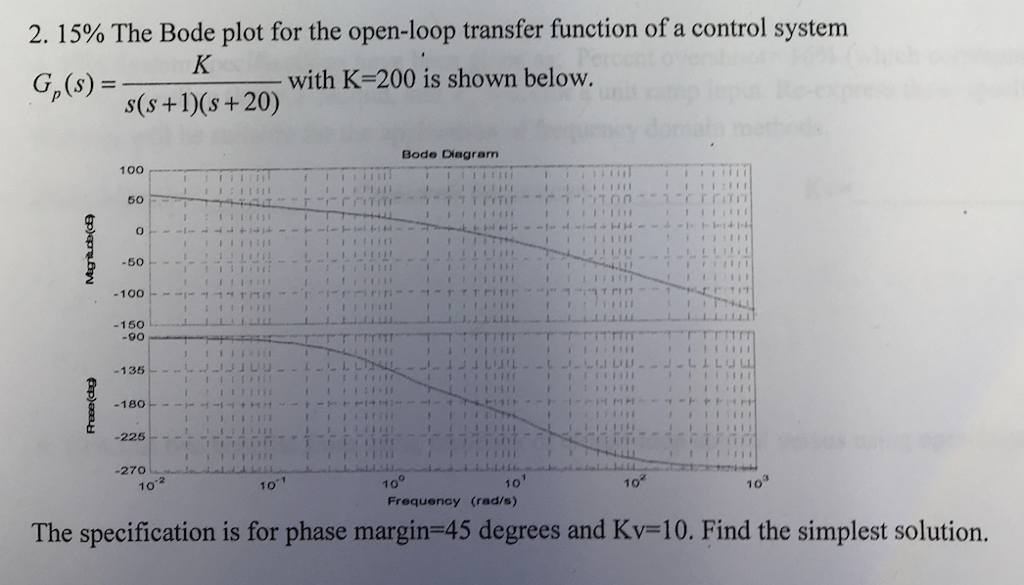
Here, we implemented the bode-plot for the comprehensive understanding of the readers. So, for very large value of ω, log magnitude of the transfer function would be Function in the frequency domain can be written as:įrom above expression, we can deduce the corner frequency or break point as


 0 kommentar(er)
0 kommentar(er)
